Ever since I was two years old, I have had a natural inclination for numbers.
My math discoveries
Magic numbers
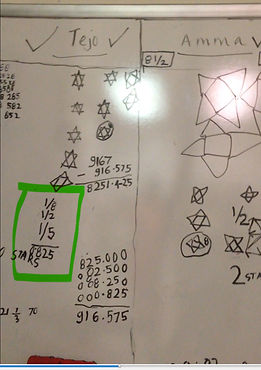
When I was five years old, I discovered that ⅛ + ½ + ⅕ is exactly 0.825. Notice that the digits are the same on both sides - 8, 2, and 5. At age 9, I proved that there are only two such magic numbers. (Can you find the other one?)
Cosine Law
I knew about the Pythagorean theorem since I was five years old. At age seven, I discovered a similar formula for triangles with an angle of 120 degrees. After a few months, I generalized this to a pattern for all angles with my knowledge of trigonometry at the time and proved it two days later. A few more years later, I read that what I rediscovered is called the Law of Cosines.
Average distance between two points on a unit line segment
At age 8, I watched a video by Presh Talwalkar on how to compute the average distance between two points in a unit square. When I saw that it used something called “integrals,” I tried an easier problem - finding the average distance between two points on a unit line segment. I asked my dad to make a spreadsheet to estimate the distance, just like Presh Talwalkar did for his problem. The results of the spreadsheet consistently showed that the average distance between two points on a line segment of length 1 is about ⅓, which I guessed was the correct answer. A few minutes later, I proved it using algebra and probability.
A year later, I learned the basics of integral calculus. I discovered that the problem of finding the average distance between two points on a unit line segment is actually a double integral in disguise. I then re-solved it using the standard techniques of integral calculus, and then by using the geometric interpretation of integrals.
Advanced Math
I study university-level math. A few classes I am taking are abstract algebra, mathematical analysis, and set theory, which are typically taught to upper-division math majors.
I have published a research paper on arXiv.
Recreational Math
During my free time, I enjoy creating and inventing math games, with Don't Be Greedy and Repeat-a-Number being the two most popular ones. Despite not being a very skilled speedcuber, I also enjoy cubing. Another one of my favorite hobbies is using a construction kit called Zometool to create intricate polyhedra that showcase beautiful geometric patterns and symmetries.
Math games
Don’t Be Greedy
This is a multiplayer game of imperfect information inspired by a game in Ben Orlin’s book Math Games with Bad Drawings. On each turn, all players jot down a positive integer without knowing what the other players are going to write. If any player is “greedy”, meaning that he/she wrote down a number more than twice the other players’ numbers, he/she gets no points for that turn. Any player who isn’t “greedy” gets the points corresponding to the number he/she wrote down. The winner is the first player to get a predetermined number of points, e.g. 1000.
Repeat-a-Number
I invented this game with my best friend Alex. In this game, there is a string of numbers, and each player extends the string by appending a number to the end based on the current last number of the string. The string starts as the single number 1. If the last number of the string is x, the player can append 2x+1, 2x+5, or the floor of x/3. The goal is to repeat a number already in the string. For more information, please see my Stack Exchange post on the topic.
Cubing
I enjoy cubing, both cubing numbers and solving Rubik’s Cubes 🙂. I solved twisty puzzles of different sizes and shapes. For some, I even found my own algorithms. Here are some puzzles I have solved before and a video of me solving a standard 3x3x3 Rubik's Cube.


Picture of me using Vieta jumping to solve a complicated math problem.
Zometool
I build shapes using a construction kit called Zometool. Here are a few mathematical shapes I have built:
The first image shows a small stellated dodecahedron (a type of polyhedral three-dimensional star). The second image shows the regular compound of five tetrahedra. The third image shows symmetric projections of hypercubes. The blue cube is a 3d cube. The small yellow polyhedron is a projection of a 4d cube. The red polyhedron is a projection of a 6d cube. The big yellow polyhedron is a projection of a 10d cube.
Answer to my earlier challenge: The only other magic number is 45!


